Kamis, 29 Agustus 2019
-Tuas-
Tuas atau pengungkit adalah salah satu contoh pesawat sederhana yang dapat berfungsi untuk memindahkan beban yang berat. Pada tuas terdapat tiga titik penting, yaitu titik kuasa (TK), titik beban (TB), dan titik tumpu (TT). Titik kuasa adalah tempat dimana gaya bekerja. Titik beban adalah titik dimana beban berada. Titik tumpu adalah tempat bertumpunya tuas. Jarak antara titik tumpu ke titik kuasa disebut lengan kuasa (LK), jarak antara titik tumpu ke titik beban disebut lengan beban (LB). Panjang pendeknya lengan kuasa sangat menentukan mudah tidaknya beban terangkat. Semakin panjang lengan kuasa semakin mudah kita melakukan usaha. Prinsip kerja tuas adalah berputar di sekitar satu titik yaitu titik tumpu.  |
| Pengertian, Rumus, Jenis Tuas |
Rumus Tuas
Dalam tuas, berlaku rumus berikut ini:
W x Lb = F x Lk
Keterangan:
- W = Berat beban (N)
- Lb = Panjang lengan beban (m)
- F = Gaya kuasa (N)
- Lk = Panjang lengan kuasa (m)
Sedangkan, untuk keuntungan mekanik tuas dirumuskan:
KM = W / F
Jenis-jenis Tuas
Ada tiga jenis tuas yang dibedakan berdasarkan letak titik kuasa, titik beban, dan titik tumpu. Ketiga jenis tuas itu adalah tuas jenis pertama, tuas jenis kedua, dan tuas jenis ketiga.
Tuas Jenis Pertama
 |
| Contoh Tuas Jenis I (Gunting) |
Tuas jenis pertama adalah tuas yang titik tumpunya terletak di antara titik kuasa dan titik beban. Contohnya gunting, linggis, dan jungkat-jungkit.
Tuas Jenis Kedua
 |
| Contoh Tuas Jenis II (Gerobak) |
Tuas jenis kedua adalah tuas yang titik bebannya terletak di antara titik tumpu dan titik kuasa. Contohnya; pemotong kertas, gerobak roda satu, dan pemecah kemiri.
Tuas Jenis Ketiga
 |
| Contoh Tuas Jenis III (Pinset) |
Tuas jenis ketiga adalah tuas yang titik kuasanya terletak di antara titik beban dan titik tumpu. Contohnya adalah pinset dan sekop.
SOAL
Sumber:https://pengertianahli.id/2015/03/pengertian-rumus-jenis-tuas.html
https://trubuswelcometo.blogspot.com/2014/02/contoh-soal-dan-pembahasan-tuas-atau.html
SOAL
Soal 1
Untuk mengangkat beban 1.000 N dipakai tuas yang panjangnya 300 cm dan lengan beban 50 cm. Hitunglah gaya yang dibutuhkan mengangkat beban tersebut!
Penyelesaian:
Soal ini ialah tuas jenis pertama, di mana titik tumpu berada di antara beban dan kuasa. Maka:
w = 1.000 N
lb = 50 cm
lk = 250 cm
w . lb = F . lk
1.000 N . 50 cm = F . 250 cm
F = 1.000 N . 50 cm/250 cm
F = 200 N
Soal 2
Sebuah linggis yang panjangnya 1,5 m dipakai untuk mencabut paku yang tertancap disebuah tembok. Linggis ditumpu 25 cm dari paku yang akan di cabut. Untuk melepaskan paku dari tembok dibutuhkan gaya sebesar 9,4 x 104 N. Berapa gaya lekat paku pada kayu? Berapa laba mekanisnya?
Penyelesaian:
misal Soal 2 ini cara pengerjaannya sama menyerupai pola soal 1. Soal ini ialah tuas jenis pertama, di mana titik tumpu berada di antara beban dan kuasa. Maka:
Fk = 9,4 x 104 N
lb = 25 cm
lk = 1,25 m = 125 cm
Fb . lb = F . lk
Fb . 25 cm = 9,4 x 104 N . 125 cm
Fb = 9,4 x 104 N . 125 cm/25 cm
Fb = 4,7 x 105 N
KM = Fb/Fk
KM = lk/lb
KM = 125 cm/25 cm
KM = 5
Soal 3
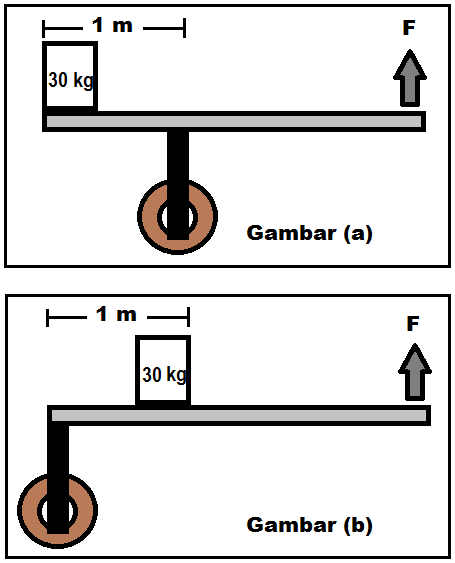
Dua orang anak yaitu Budi dan Iwan didiberikan sebuah roda dan papan yang panjangnya 3 m yang akan dipakai untuk mengangkat sebuah benda yang massanya 30 kg (jika percepatan gravitasi ditempat tersebut 10 m/s2). Budi menyusun papan tersebut menyerupai gambar (a) sedangkan iwan menyusun papan tersebut menyerupai gambar (b) di bawah ini.
Siapa yang memerlukan gaya paling kecil unuk mengangkat benda tersebut? Jelaskan! Berapa laba mekanis masing-masing sistem?
Penyelesaian:
Untuk mengetahui siapa yang memerlukan gaya paling kecil, harus dicari gaya angkat untuk masing-masing sistem. Untuk sistem gambar (a) ialah tuas atau pengungkit jenis pertama, di mana titik tumpu berada di antara beban dan kuasa, maka:
m = 30 kg
lb = 1 m
lk = 2 m
g = 10 m/s2
w . lb = F . lk
m . g . lb = F . lk
30 kg. 10 m/s2. 1 m = F . 2 m
300 N.m = F . 2 m
F = 300 N.m/2 m
F = 150 N
Keuntungan mekanis untuk sistem (a) yakni:
KM = w/F
KM = 300 N/150 N
KM = 2
Untuk sistem gambar (b) ialah tuas atau pengungkit jenis kedua, di mana beban berada di antara titik tumpu dan kuasa, maka:
m = 30 kg
lb = 1 m
lk = 3 m
g = 10 m/s2
w . lb = F . lk
m . g . lb = F . lk
30 kg. 10 m/s2. 1 m = F . 3 m
300 N.m = F . 3 m
F = 300 N/3
F = 100 N
Keuntungan mekanis untuk sistem (b) yakni:
KM = w/F
KM = 300 N/100 N
KM = 3
Jadi, yang mengeluarkan gaya paling kecil ialah Iwan yaitu 100 N sedangkan Budi mengeluarkan gaya 150 N. Keuntungan mekanis untuk sistem gambar (a) ialah 2, sedangkan laba mekanis untuk sistem gambar (b) ialah 3.
Soal 4
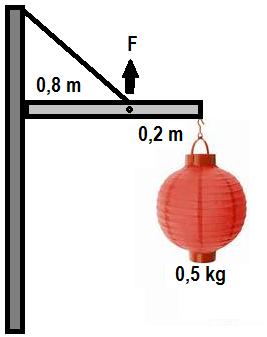
Sebuah lampion mempunyai massa 0,5 kg digantung dengan memakai kayu dengan panjang 1 m dan masanya diabaikan, menyerupai gambar di bawah ini.
Hitunglah gaya angkat F minimal supaya lampion supaya lapion tidak jatuh (jika percepatan gravitasi ditempat tersebut 10 m/s2)!
Penyelesaian:
Soal ini ialah tuas jenis ketiga, di mana kuasa berada di antara beban dan titik tumpu. Maka:
m = 0,5 kg
g = 10 m/s2
lb = 1 m
lk = 0,8 cm
w . lb = F . lk
m . g . lb = F . lk
0,5 kg . 10 m/s2 . 1 m = F . 0,8 cm
F = 5 N.m/0,8 cm
F = 6,25 N
Jadi gaya angkat F minimal yang harus dikeluarkan supaya lampion tidak jatuh ialah 6,25 N
Sumber:https://pengertianahli.id/2015/03/pengertian-rumus-jenis-tuas.html
https://trubuswelcometo.blogspot.com/2014/02/contoh-soal-dan-pembahasan-tuas-atau.html
